※この記事は、連載【はじめての和声法】と【はじめての対位法】に共通する導入部分です。
音程の知識を深める
前回の記事では音程について学びました。
音程とは音と音の距離のことで、それは2度や4度というように表すことができました。さらに音程には細かい分類の仕方があります。 今回は音程に関する知識をさらに深めましょう。
最小の音程=半音
まずは、半音と全音について学びましょう。
半音とは、「最も小さい音程」のことです。音程が最小であるということは音同士の隔たりが最も短いということで、つまり隣り合う音であるということです。ピアノの鍵盤を思い浮かべると分かりやすいでしょう。
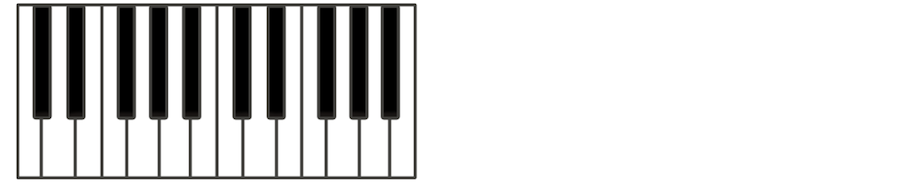
たとえば、Cと最も近く隣り合う音はどの音でしょうか。半音関係にある音は2つあることになります。低い方の音と高い方の音です。
まず、Cから半音関係にある低い方の音はHです。では、高い方の半音関係にある音はどの音でしょうか?
Cと半音関係を持つ高い方の音は Cis(Des)です。Cと半音関係にある音はDであると間違えることがよくあるのですが、鍵盤上で見て分かるように、CとDの音の間には、黒鍵の音があります。この黒鍵こそが、Cと半音関係にある音なのです。
では、半音についてもう一つの例を見てみましょう。Esと半音関係の音はどの音でしょうか。それはDとEということになります。このように、黒鍵が基準であったとしても、半音の関係の音とは最も近く隣り合う音となります。
全音は、半音2つ分の音程です。
例として、Eの全音関係の音を探してみましょう。まず、低い方の全音はDとなります。
では高い方の音はどの音でしょうか? 半音2つ分が全音となるので、Fisとなります。ここでは、FはEとは半音関係なので、Fからさらに半音上げた音が、全音関係の音になります。ですから、Eと全音の関係にある高い方の音はFisとなるのです。
ここまで理解できたら、次の問題を解いてみましょう。表を埋めてください。
練習問題1
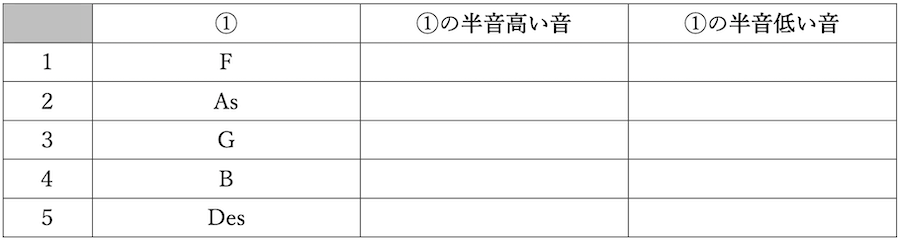
練習問題2
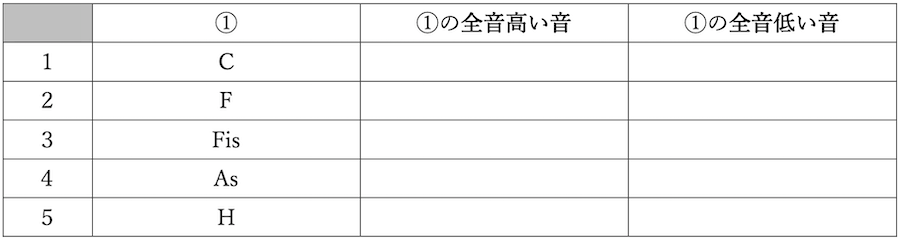
練習問題1の答え
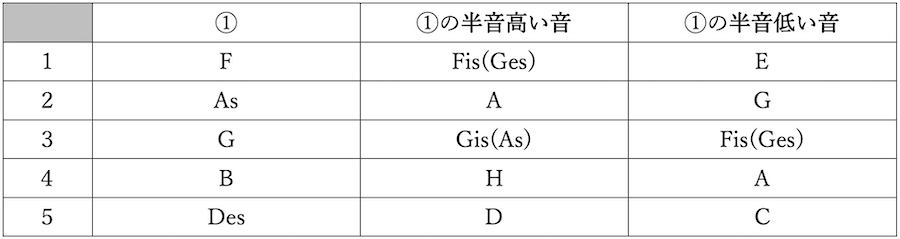
練習問題2の答え
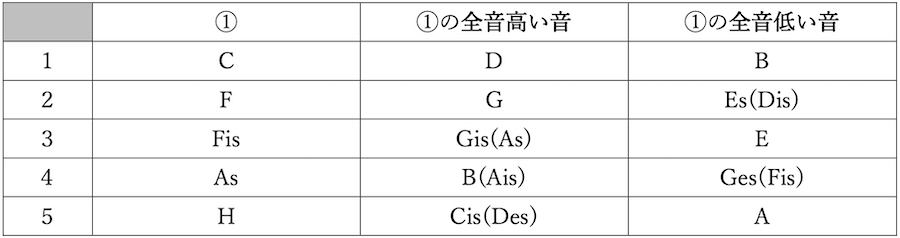
音程のいろいろな個性
音程についてさらに学んでみましょう。まず、次の譜例を見てください。
譜例1

この譜例の1、2、3の和音は、全て5度の和音です。しかし2と3の和音は、それぞれにシャープやフラットがついています。そうなると楽譜上では同じ5度でも、鍵盤上では音と音との隔たりは、より長くなったり短くなったりします。
この違いは、厳密に分けなければいけません。そのために、基準となる和音を見つけなければいけません。
譜例1で言うと、1の和音が基準となる5度になります。この基準となる5度のことを「完全5度」と言います。完全5度は、半音を7つ分隔たった音で作ることができます。
ところで、なぜこの音程を「完全」であるとするのでしょうか。それは、この音程の振動数比が単純で、その響きもよく溶け合うとされているためです。そのような音程のことを完全音程、もしくは完全協和音といい、完全音程には完全5度の他、完全1度、完全4度、完全8度の3つあります。
完全音程であるかどうか見分けるためには、半音がいくつ分隔たっているのか数えてみる必要があります。最初は少し時間がかかりますが、慣れてくると一目で識別することができます。次の表を参考にしましょう。
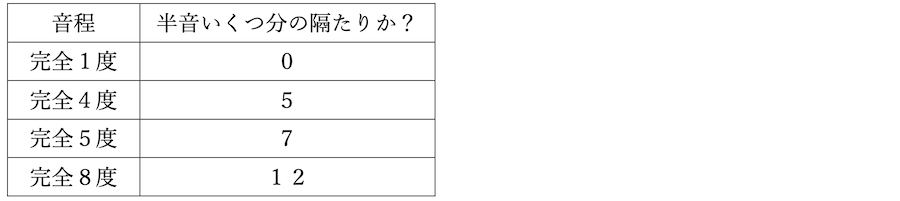
それでは、次の問題を解いてみましょう。完全音程のみをチェックしましょう。
練習問題3

答え:完全音程は1、3、6、7、8、10、12
完全音程について理解できたら、それを基準にして音程を分けることができます。完全音程より半音1つ分音程が広くなれば増音程、狭くなれば減音程と呼ばれます。次の譜例を見てみましょう。
譜例2

この譜例の1の和音は、Gにシャープが付きGisになっています。本来CとGの音程は完全5度なのですが、シャープが1つ付いているため、完全音程でなくなっています。
ピアノの鍵盤上で考えると分かりやすく、GがGisになることによって完全音程よりも音程が広くなっています。そのためこの音程は「完全」ではなく、「増」となり、増5度の音程となります。
それでは、2の和音はどうでしょうか。この和音はGにではなく、Cにシャープが付いています。それによってこちらは完全5度よりも狭くなっています。これを減5度といいます。
完全音程から半音が1つ分広くなると増音程、狭くなると減音程といいますが、半音が2つ分、つまり全音1つ分広くなると重増音程、狭くなると重減音程といいます。
それでは次の問題を見て、それぞれの音程を書いてみましょう。
練習問題4

答え:1.完全4度/2.増5度/3.減5度/4.完全8度/5.完全5度/6.増4度/7.増5度/8.減5度/9.増4度/10.完全8度/11.増8度/12.重増4度
ところで、完全音程は1度、4度、5度、8度の4つだけだと説明しましたが、その他の2度、3度、6度、7度はどのように分けるのでしょうか。次の譜例を見てみましょう。
譜例3

このように、同じ6度でもいろいろな6度がありそうです。2度、3度、6度、7度は完全音程ではなく、長音程と短音程になります。それらも半音がいくつ隔たっているのかで識別できます。次の表を見てみましょう。

完全音程と同じように、初めは時間がかかりますが、次第に識別が簡単にできるようになります。それでは次の問題を解いてみましょう。長音程のみをチェックしましょう。
練習問題5

答え:長音程は1、2、3、6、8、9、11、12
長音程と短音程を識別できるようになったら、完全音程と同じように、それを基準にして音程を分類します。
譜例4

この譜例では、1の和音は長3度となっています。2の和音はAにシャープが付いていますので、長3度よりも半音1つ分広くなっていることになります。そうなると、完全音程の場合と同じように増音程となり、増3度となります。
それでは、3の和音ではどうでしょうか。ここではFにシャープが付いて、長3度よりも半音1つ分狭くなっています。完全音程の場合だと音程が半音1つ分狭くなると減音程となりますが、長音程の場合だと短音程となります。3の和音は短3度となります。
それでは、4の和音ではどうでしょうか。3の和音のAにシャープが付いている状態になっています。この場合、3が短音程でしたが、短音程から半音1つ分広くなっています。そうなると長音程になるのです。つまり4の和音は長3度です。
5の和音は、3の短3度の和音よりもさらに狭くなっています。この場合は減3度となります。
つまり、長音程より半音1つ分広くなると増音程になり、狭くなると短音程になります。そして、短音程より半音1つ分広くなると長音程となり、狭くなると減音程になるのです。
さらに、完全音程の場合と同じように、増音程より半音1つ分広くなると重増音程となり、減音程より半音1つ分狭くなると重減音程となります。
最後に、今回触れた音程について課題を出します。それぞれの音程を書いてみましょう。
課題3

また、前回の課題2の答えも載せます。

答え:1.7度/2.4度/3.7度/4.5度/5.2度/6.10度(1オクターヴと3度)/7.6度/8.3度/9.17度(2オクターヴと3度)/10.4度/11.2度/12.5度
まとめ
今回は音程についての知識を深めました。音程には完全音程、長音程、短音程、そして増音程、減音程、重増音程、重減音程があることを学びました。それぞれの関係を表にすると、次のようになります。
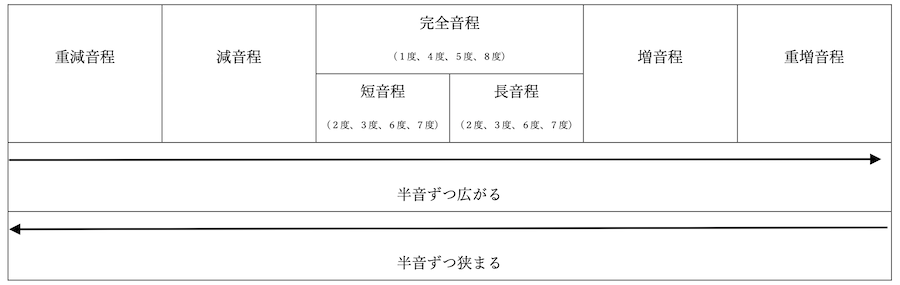
初めは音程の識別に時間がかかりますが、音程はとても大事なポイントになりますので、何度も復習して慣れるようにしましょう。



